高级算法与工程

Machine Learning - Android Ng

4.1. 评价 ml 系统

计算测试误差的函数就是减去正则化项的损失函数

4.1.1. 选择模型

把数据集分为训练集、测试集和交叉验证集
- 中心思想：更加公平（不是更加准确）
先选择交叉验证误差最小的模型
可以使用测试集误差来代表泛化误差，评估模型的泛化误差

训练集在不同的模型上拟合出每个模型的最优 WB_，_交叉验证集用来选择不同的模型_，_测试集用来检验该模型的好坏效果（误差）

4.1.2. 诊断模型

如何决定第二步做什么，以提高学习的效果
方法：观察算法的偏差和方差（Bias and Variance）
$J_{train}$很高时，往往意味着 Bias 高（欠拟合）
$J_{cv}$高时，且$J_{cv}$比$J_{train}$高很多时，往往意味着 Variance 高（过拟合）

$J_{cv}$和$J_{train}$都比较低时，是比较理想的

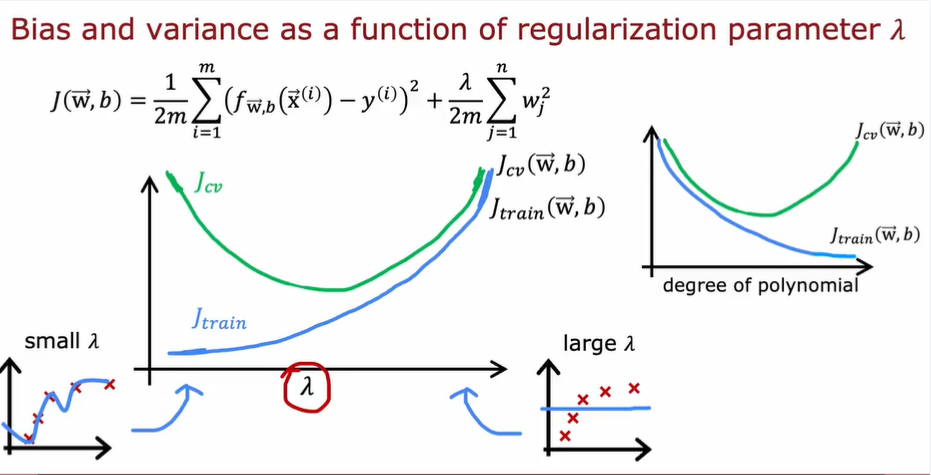
4.1.4. 选择正则化参数 λ

λ ~ w 的值 ~ J

测试过程如下，选择$J_{cv}$最小的模型

λ 和$J$的关系

4.1.4. 如何评价模型错误率

与其直接看误差，不如以人类水平为基准进行评判

4.1.4.1. 性能基准

人类水平（常用于非结构化数据，如图像、语音、文本）
竞争对手的算法表现
经验

基准线水平
训练误差($J_{train}$)
交叉验证误差($J_{cv}$)
前两者之间的差 indicates bias，后两者之间的差 indicates variance

一般 4%以上的差距就认为很大了

4.1.5. 学习曲线

4.1.5.1. debug 算法的方法

方法	解决
更多训练集	高方差
尝试更小的特征集	高方差
增加特征	高偏差
增加多项式项数	高偏差
减少 λ	高偏差
增加 λ	高方差

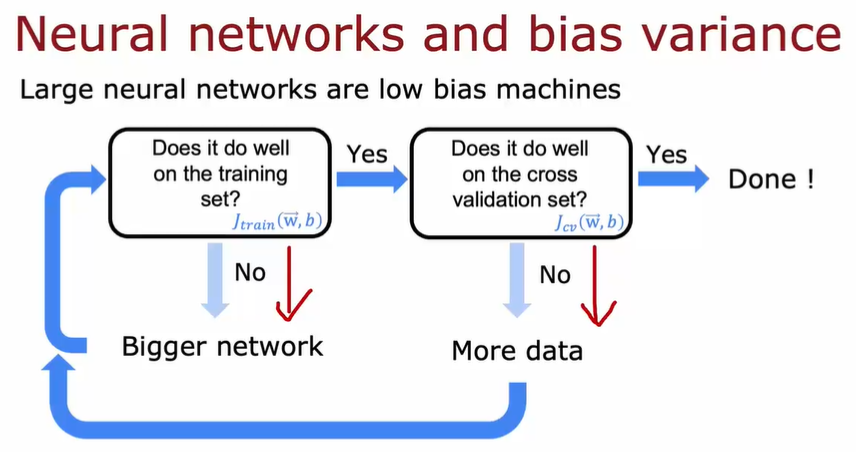
4.1.5.2. 神经网络应用

我们往往需要在 keep a balance between bias and variance. 但是神经网络给我们提供了一个全新的视角和方法。它可以自动帮我们完成权衡。具体解释如下：

tf 代码

4.1.5 误差分析

人工检查 100 个数据集，并将它们按照共同特征分类
然后进行一些针对性补丁，比如添加一些更加具有针对性的数据集

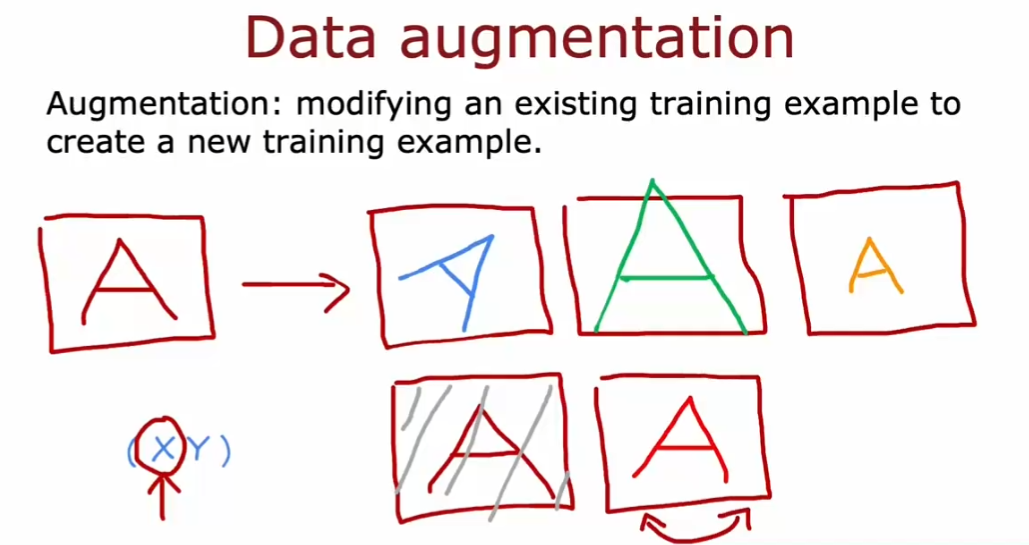
4.2. 数据增强

Data argumentation
通过已有的训练集来进行新的训练：比如把训练集 A image 进行一些变化，然后重新进行训练（人为的增大训练集）
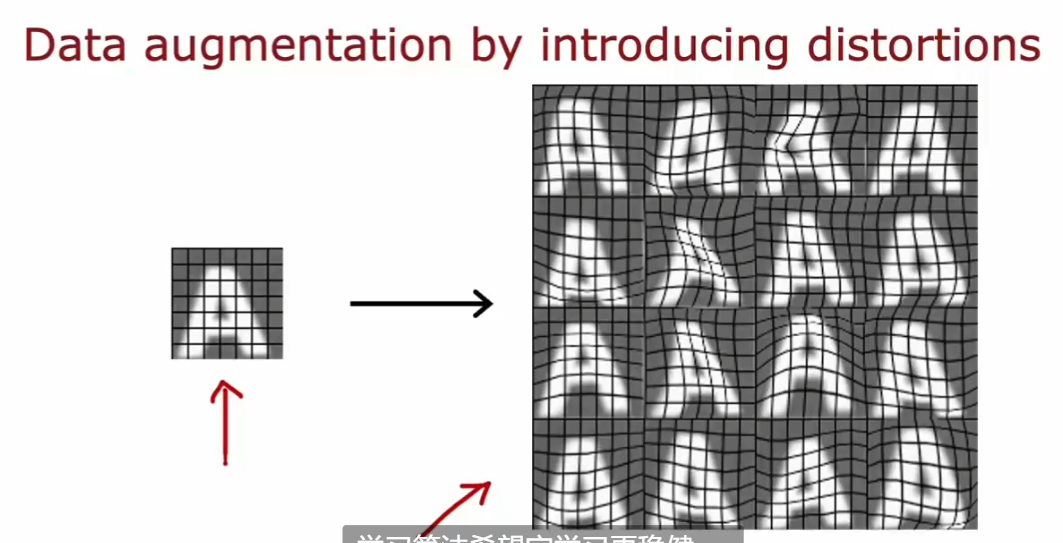
- 注意：对数据所作的改变和扭曲，应该是测试集中噪声或变形的代表
  - 随机无意义的噪声和扭曲是没有意义的
广泛的应用于图像和音频中

4.3. 迁移学习

可以用来自不同任务的数据完成学习
应对数据少或数据难以获取的情况

以下图为例：先在有 1 million 个数据的训练集上训练出可以识别 1000 个类别的神经网络（比如猫、狗等等…），随后保持上述神经网络除了 output 层外的参数不变（把上述神经网络除了 output 层 copy 一遍），迁移到拟训练的数据集上进行训练。训练有两种选择：

只训练 output 层的参数
训练所有参数。但是以 copy 的神经网络参数作为初始值

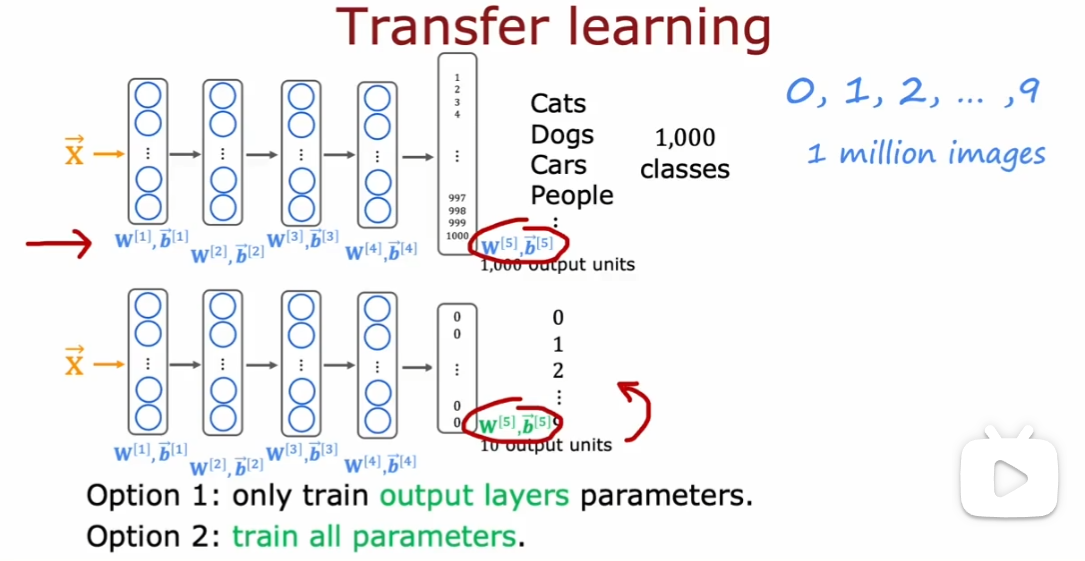
先在大型数据集上进行训练，然后在较小的数据集上进一步参数调优，这两个步骤称为监督预训练（supervised pretraining）
然后运行梯度下降等算法在新数据集上，进行微调（fine tuning）

需要注意的是：预训练的神经网络必须和最终需要的神功网络是同一类型的。比如要训练图像相关的神经网络，必须使用图像相关的预训练神经网络

4.4. 构建 ml 系统的周期

确定项目范围
收集数据
训练模型
部署模型

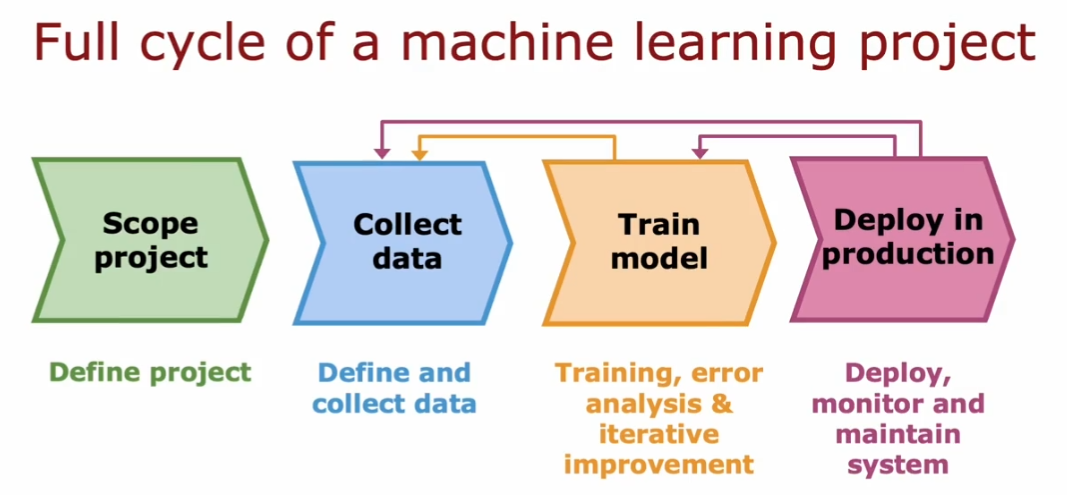
4.4.1. MLOps

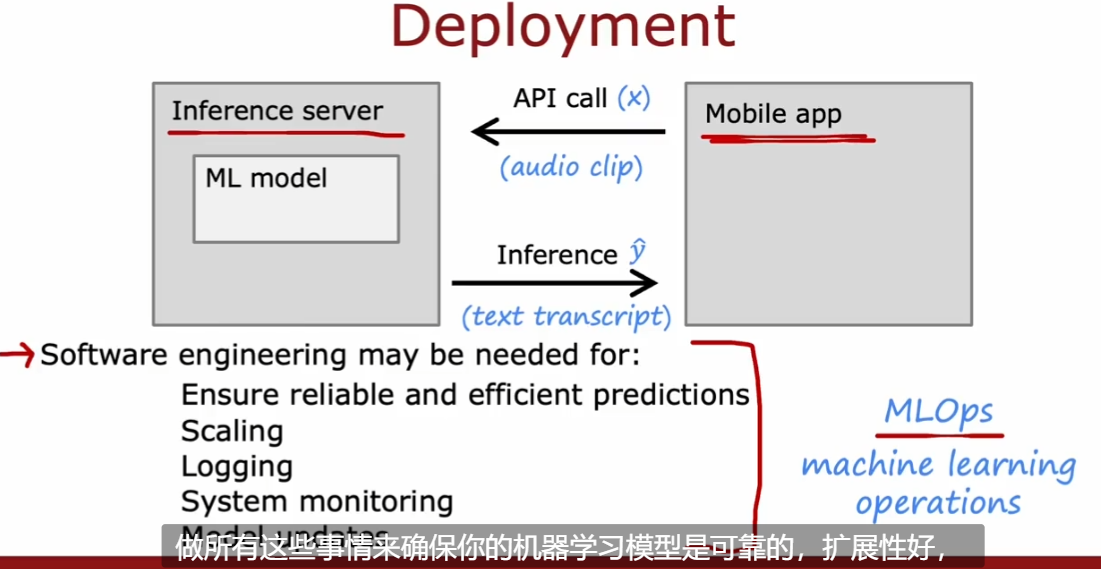
有点类似 DevOps

4.5. 数据倾斜

评价一个罕见类的学习算法性能
- 构造混淆矩阵（2 * 2 矩阵）
- 精度（Precision）：评价算法是否准确：当算法诊断有病时，确诊的概率
- 召回率（Recall）：评价算法对真正病人是否有用（样本中的正例有多少被预测正确了或找的全）

4.5.1. Trade off between P and R

提高 threshold 会提高 Precision，降低 Recall

建议根据具体的应用场景进行权衡

4.5.1.1. F score

权衡 Recall 和 Precision 的参数

$$
F_1 \ scrore = \frac{1}{\frac{1}{2}(\frac{1}{P} + \frac{1}{R})} = 2\frac{PR}{P+R}
$$

这个式子会关注二者中较小的部分（其实就是 P 和 R 的调和平均值）

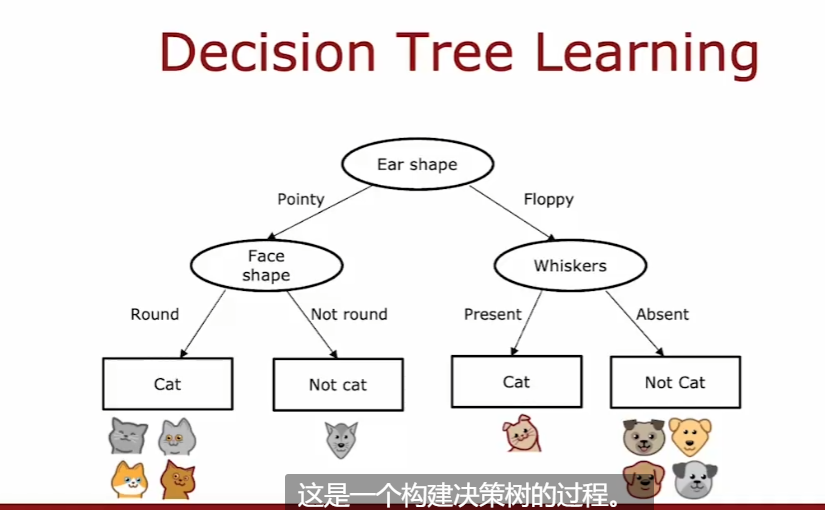
4.6. 决策树

Decision Tree

4.6.1. 步骤

选择根节点的特征
选择在每个节点上区分的特征（为了最大化的分类，保证分类纯度 purity）
何时停止树的划分（stop splitting）
- 当结点里 100%都是同一类
- 当分裂（split）结点会导致树超过最大深度
- 当分裂（split）后对纯度产生的增益小于阈值（threshold）
- 当结点里 examples 的数量小于阈值（threshold）

4.6.2. 熵

entropy
度量样本不纯程度

$$
p_0 \ = \ 1\ - \ p_1 \
H(p_1) = -p_1log_2(p_1) - p_0log_2(p_0) \
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = -p_1log_2(p_1) - (1-p_1)log_2(1-P_1) \
Note: 0log(0) = 0
$$

4.6.2.1. 如何利用熵度量 node

使用加权平均。因为我们认为分到了较多 examples 的分支的熵是更重要的

4.6.2.2. 信息增益

根节点的熵 - 子节点的加权平均熵

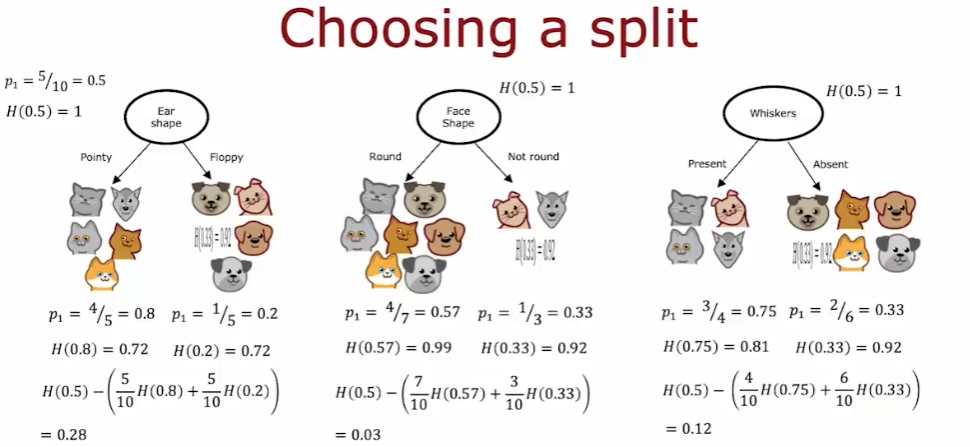
计算公式

4.6.4. Decision Tree Learning

building decision tree 是一个递归过程

4.6.5. one-hot 编码

用于处理不止 2 种取值的离散变量

如果一个分类特征有 k 种可能的取值，那么把这 k 种特征按照 0、1 进行编码取值

如果看任何一行，总有一个特征是 1，因此称之为 one-hot（独热）编码
one-hot 编码不仅适用于决策树，还适用于神经网络

4.6.6. 处理连续变量

对连续变量进行划分处理（分类），即将连续变量区间设置阈值，将其分为 2 个子集
分类的标准是谁贡献了更大的信息增益
一般划分值的候选方法是：将值 list 排序，然后取所有值之间的中点

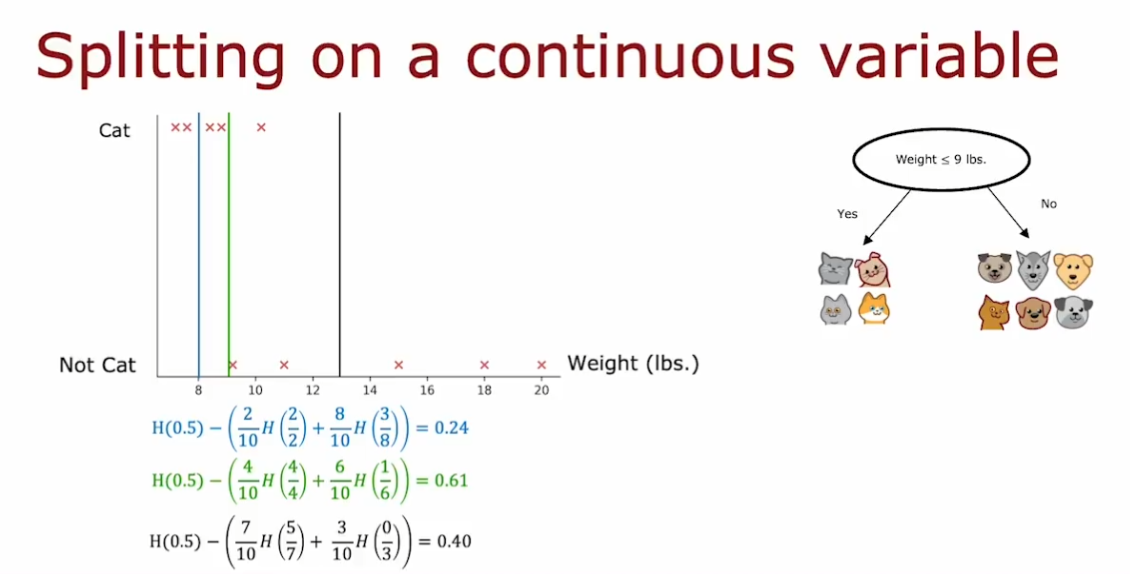
4.7. 回归预测中的决策树

决策树会根据叶子结点中样本数据的平均值做出预测

在回归预测中，决定结点选择哪种划分策略的标准不再是熵，而是带权方差（variance）
就像最终决策树的衡量公式是信息增益，我们在这里计算的也实际上是方差减少量

4.8. 决策树集合

使用单个决策树的缺点是：其对数据的微小变化非常敏感。(一旦数据微小变化，那么结点的信息增益可能会变化很多，从而导致决策树变的完全不同)
- 解决方法：构建更多的决策树，即决策树集合，使得预测结果更健壮
使用树集合，然后都运行数据，进行预测。多数的结果即为预测结果。

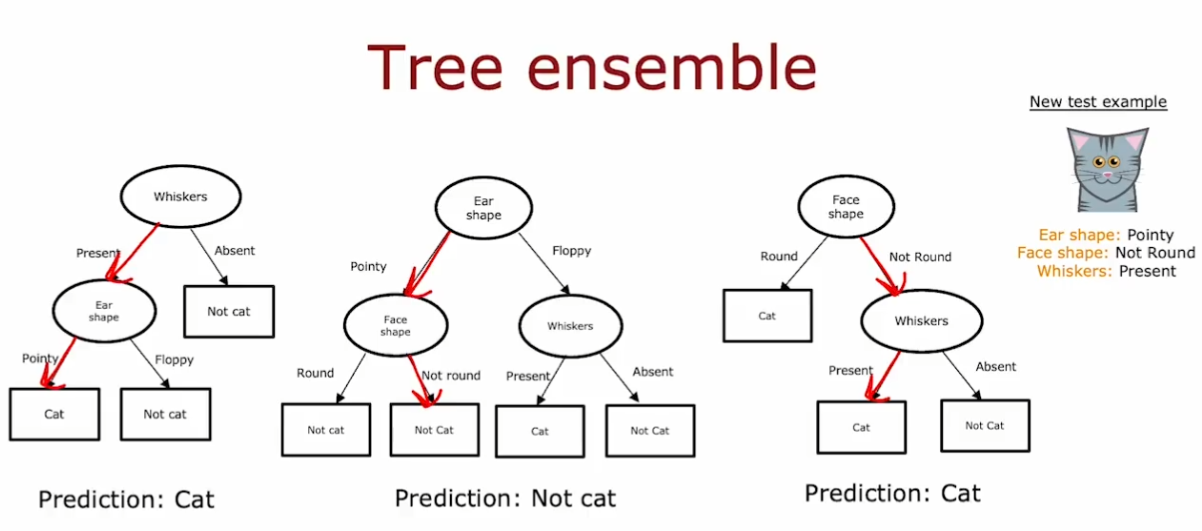
4.8.1. 有放回抽样

Sampling with replacement

4.8.2. 随机森林算法

4.8.2.1. 袋装决策树算法

对于一个大小为 m 的训练集
- 使用有放回抽样获得同样大小为 m 的训练集，然后训练出一个决策树
- 重复以上过程直到训练出需要的决策树数量（一般是 100，记为**B**）
问题
- 根节点及其附近的特征仍然相似
- 导致算法不够精确，需要改进

4.8.2.2. 改进成随机森林算法

在每个结点中，当需要选择一个特征来 split node 时，如果有 n 个特征可以选择，那么我们每次随机选择k（k < n ）个特征构成 n 个特征的子集，让算法在这个子集中进行选择（即计算信息增益然后进行 split）
比单一决策树更健壮的原因是：随机森林算法探索了更多训练集微小变化的可能，能够对有放回取样过程导致的所有数据变化进行平均，使得训练出来的模型更 robust

4.8.3. XGBoost 增强决策树算法

非常类似于针对性训练，比如刻意训练不熟练的一段，而不是总是训练整首曲子

XGBoost（eXtreme Gradient Boosting）
- 增强决策树的一种开源实现
- 高效
- 对默认拆分条件有很好的选择
- 内置正则化以防止过拟合
- 和 dl 一样，是算法竞赛的热门算法

4.9. 决策树和神经网络的使用时机

决策树和树集合
- 对表格化（结构化）tabular（structured）数据表现很好
- 不建议在非结构化数据上使用（图像、音频、文本）
- 训练迅速
- 小的决策树可能是人类可以理解的（可解释性）
神经网络
- 对结构化和非结构化数据都表现良好
- 比决策树慢（训练时长等）
- 可以使用迁移学习（而决策树不行）
- 当构建多个模型共同协作的系统时，神经网络模型更容易串在一起（决策树一次只能训练一个）

May 23, 2022

Coursera: ML04-高级算法与工程