逻辑回归与正则化

Machine Learning - Android Ng

2.1. 逻辑回归

• 使用 0 和 1 来代表 negative 和 positive

2.1.1. Sigmoid 函数

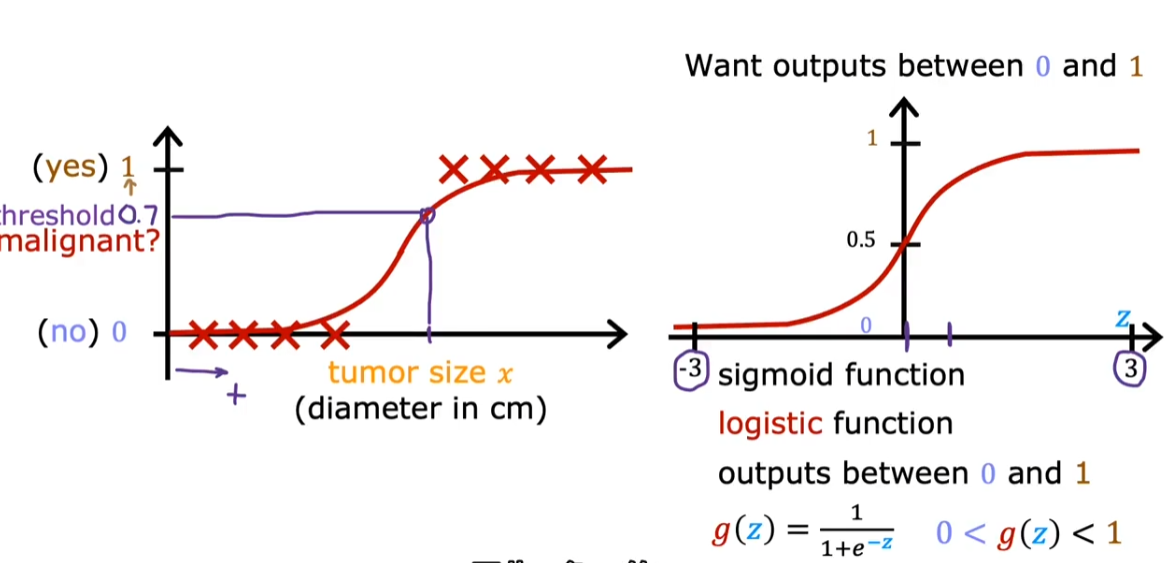
• 通常将函数作为输入，然后输出[0,1]

2.1.2. 决策边界

当我们把$wx+b$作为自变量输入 sigmoid 函数时，假设我们取 0.5 作为 sigmoid 函数的分界点（大于 0.5 认为是 positive，小于 0.5 认为是 negative），我们可以推导出：

$$
wx + b \gt 0
$$

是 positive，从而我们抽象出

$$
wx + b = 0
$$

作为决策边界

当然决策边界也可以是非线性（多项的）

2.1.3. 代价函数

• 关键之处是原来的平方误差损失函数作用在 sigmoid 函数后不再是凸函数了（convex-function），导致梯度下降不好作用。
• 因此需要找到一种是凸函数的代价函数

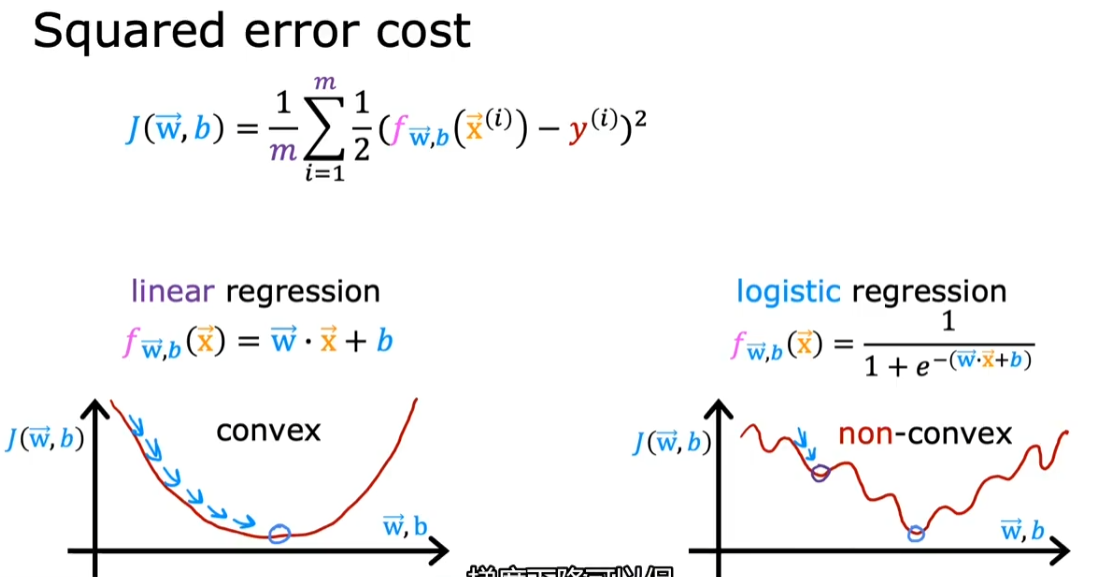
• 因此找到如下损失函数：

2.2. 实现梯度下降

• 梯度下降的大公式是一样的，但是求导的细节有不同 👇

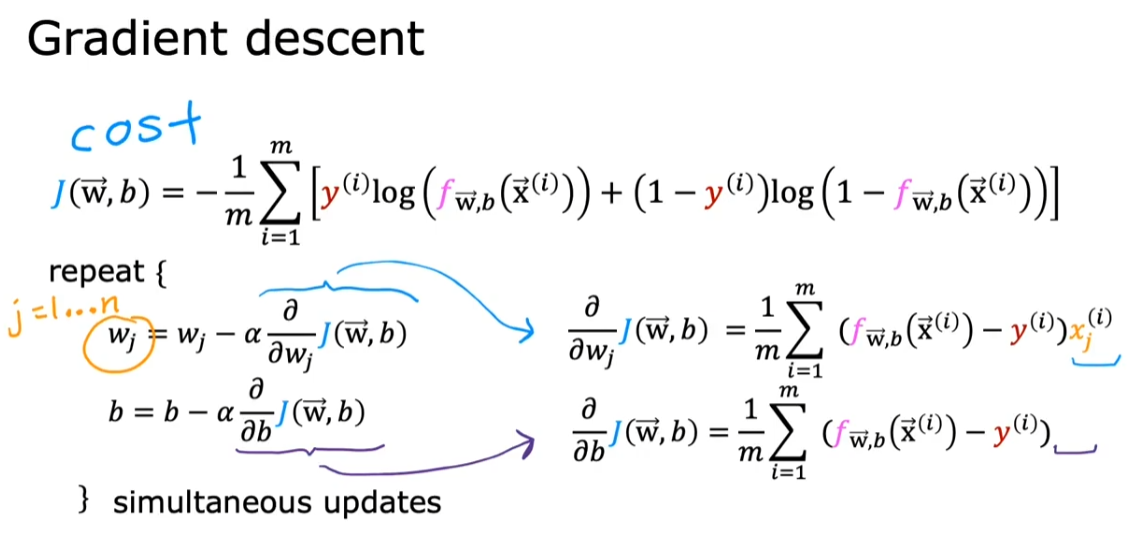
2.3. 过拟合

• overfitting / high variance

• 过于贴近训练集，导致实际预测结果的不准确（如下图右三）

2.3.1. debug / address methods

• 收集更多的训练数据
• 考虑使用较少的特征
  • 选择最相关的特征（最小的特征子集）
  • course 2 会学习自动特征的算法
• 正则化（Regularization）
  • 保留所有的特征，但尽量避免它们产生过拟合
  • 把一些特征的参数调小（接近 0）
  • 是否正则化 b 对实际模型的影响不大（一般不正则化 b）

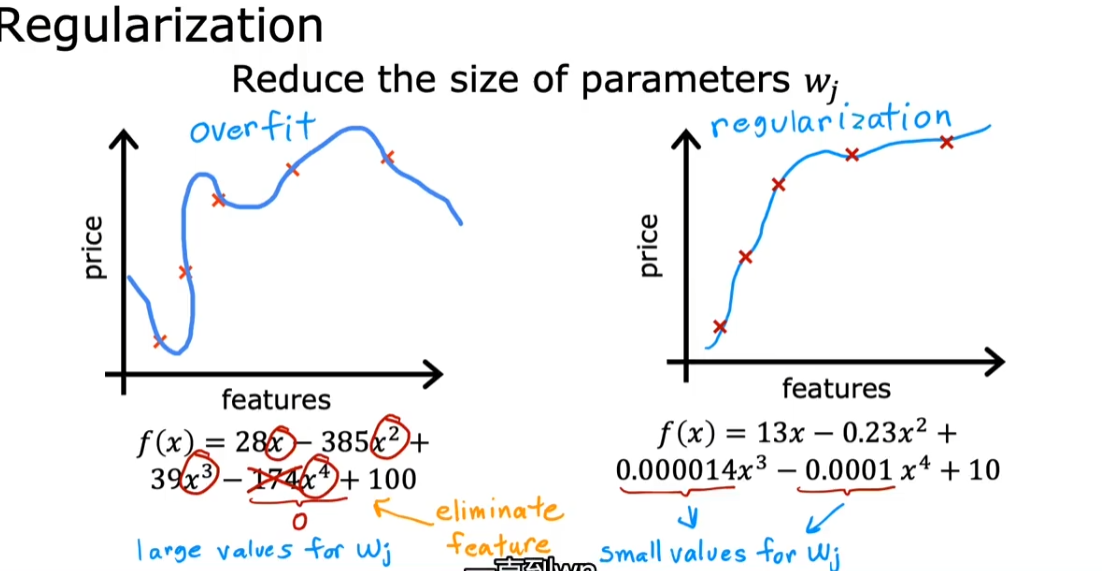
2.4. 正则化

• 正则化的思想是：如果有很多特征，我全部使用的话可能会造成过拟合，而我也不知道哪些特征是重要的，哪些是不重要的，那么我就对所有的这些特征进行建模，并对他们进行正则化奖励或惩罚（penalize）。不重要的参数会被惩罚的非常小。从而得到不那么容易过拟合的模型

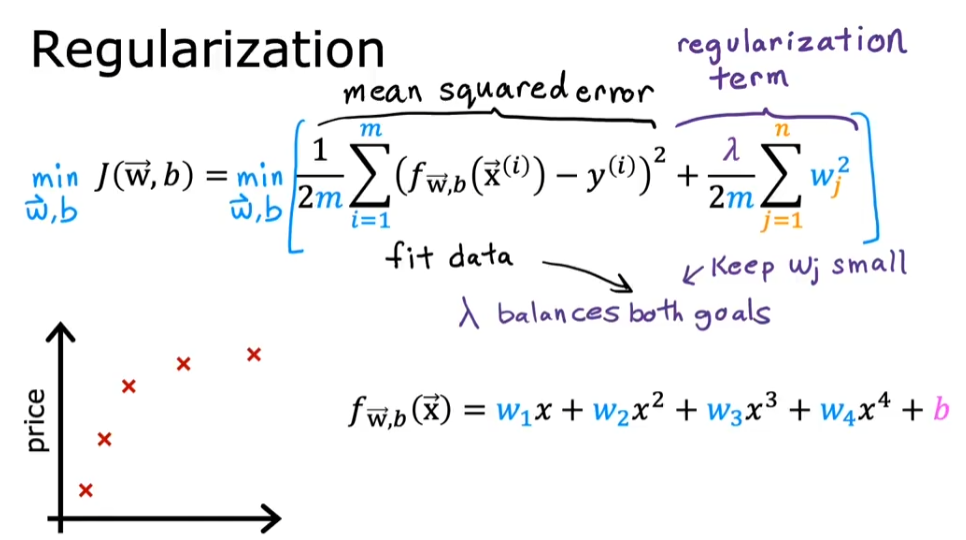
• 公式

• 注意：λ 下面有分母 2m。这样可以保证当 m（训练集样本）增大时，先前的 λ 仍然有用
• 加入正则化后的 cost function，前一项是为了让模型拟合数据，而后一项是为了防止模型过拟合。参数 λ 平衡了这两个功能。我们往往需要选择一个权衡两者的 λ

2.5. 加入正则化后的梯度下降

2.5.1. 线性回归

• 加上正则化之后，使得每次梯度下降后的$w_j$下降一点点

2.5.2. 逻辑回归

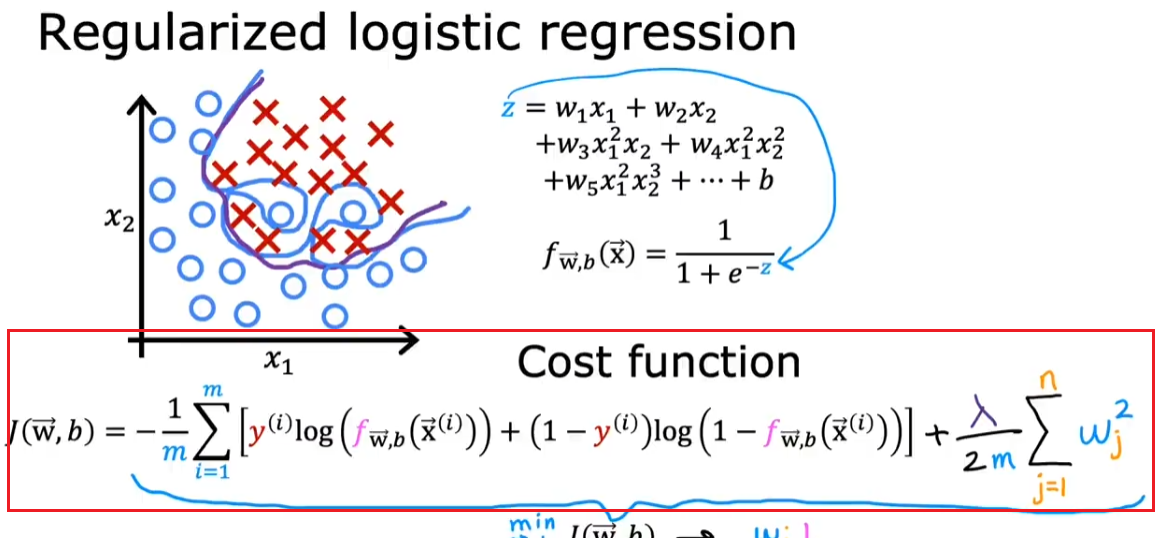
• 求导之后的梯度下降更新项和线性回归一模一样