概论与线性回归

Machine Learning - Android Ng

1.1. 分类

监督学习
无监督学习
增强学习（reinforcement learning）

1.2. 监督学习

supervised learning
通过给予机器正确的例子（包括答案）让其学习

1.2.1. 回归

regression
从无限多个可能的 output 中预测一个结果（连续），output 一般是数字

1.2.2. 分类算法

classification
和回归的区别是：只有两个或有限的可能的输出
预测类别，而类别不一定是数字

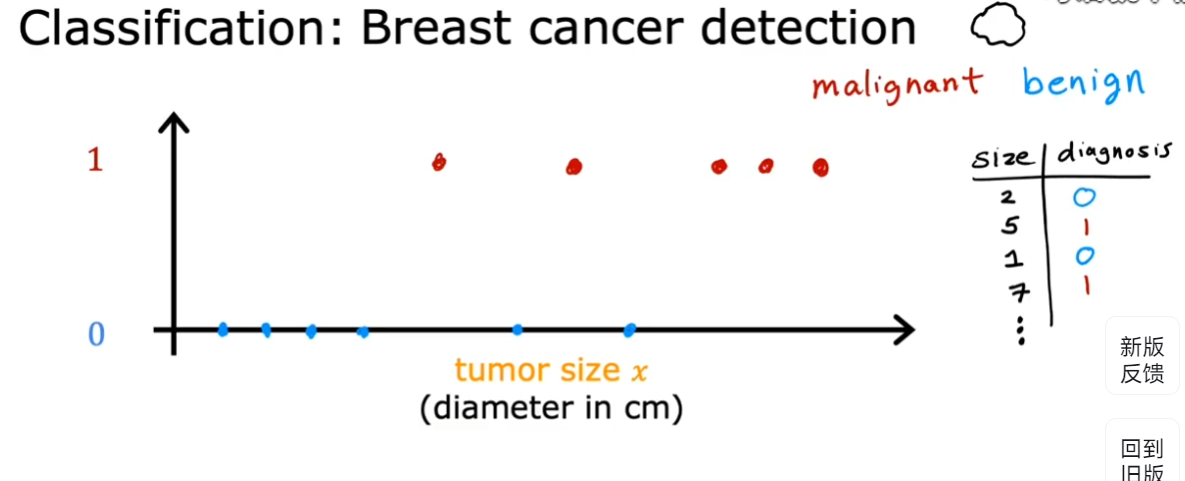
上图例子（预测乳腺癌）中，只有肿瘤大小一个输入。但实际上可以有多个输入

1.3. 无监督学习

Unsupervised learning
在无监督学习中，得到的数据是无 label 的，即无结果
目的只是找到一些数据中的模式或结构，而不是得到什么具体的结论

1.3. 1. 聚类

clustering
获取没有标签的 data，并试图自动将他们分到不同的类别（聚簇）中

1.3.2. 异常检测

Anomaly detection

1.3.3. 降维

Dimensionality reduction

1.4. 线性回归模型

属于监督学习

1.4.1. 数据表

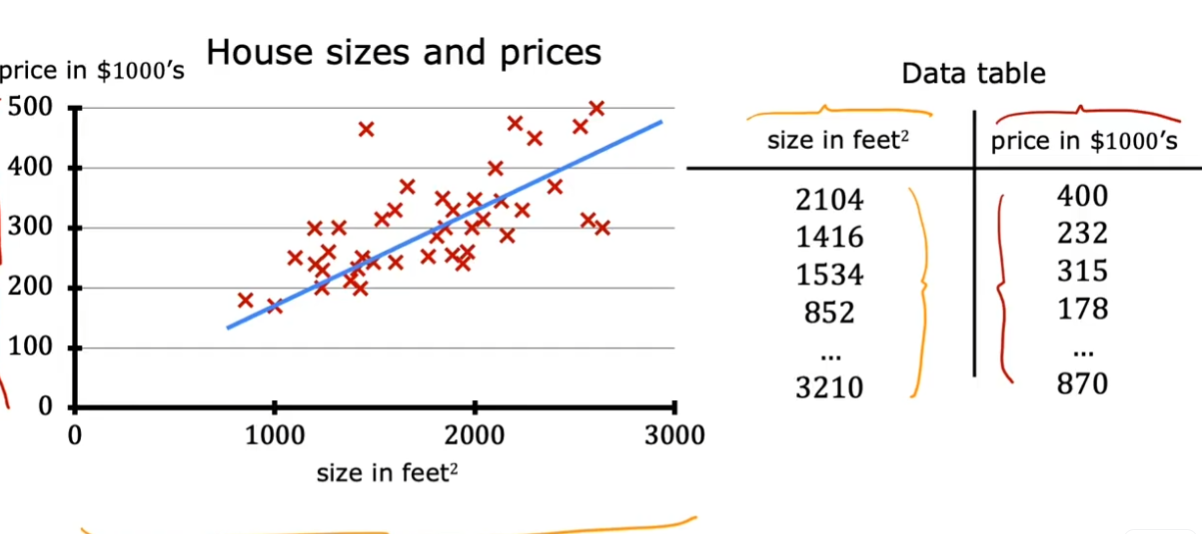
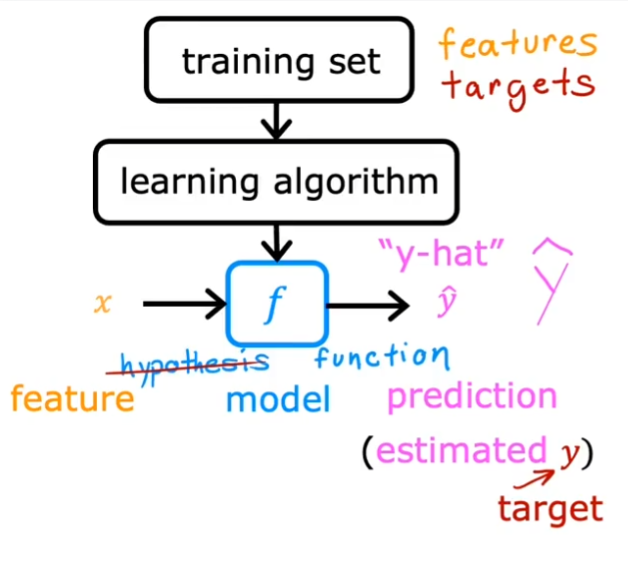
1.4.2. 训练集

用来训练模型的数据，包括输入（变量、特征或输入特征）和输出（目标变量）

一些专业术语

1.5. 成本函数

$$
J(w,b) = \frac{1}{2m} \Sigma_{i=1}^m (y_{hat}^{(i)} - y^{(i)})^2
$$

平方残差损失函数常常用于线性回归中。我们希望找到一个模型让损失函数最下

1.6. 梯度下降

gradient descent

$$
min_{w_1,….,w_n,b}J(W_1,W_2,…,W_n,b)
$$

对应多参数的损失函数，可以使用梯度下降找到使其最小的点。

注意：如果对于一些不是吊床形和碗形的图像，可能存在不止一个极小值

选择一个 w 和 b 作为起始点
然后沿着斜率最陡的方向下降

$$
w = w - \alpha \frac{\alpha}{\alpha w}J(w,b)
$$

$$
b = b - \alpha \frac{\alpha}{\alpha b}J(w,b)
$$

$\alpha$叫做学习率

一个例子

1.6.1. 学习率

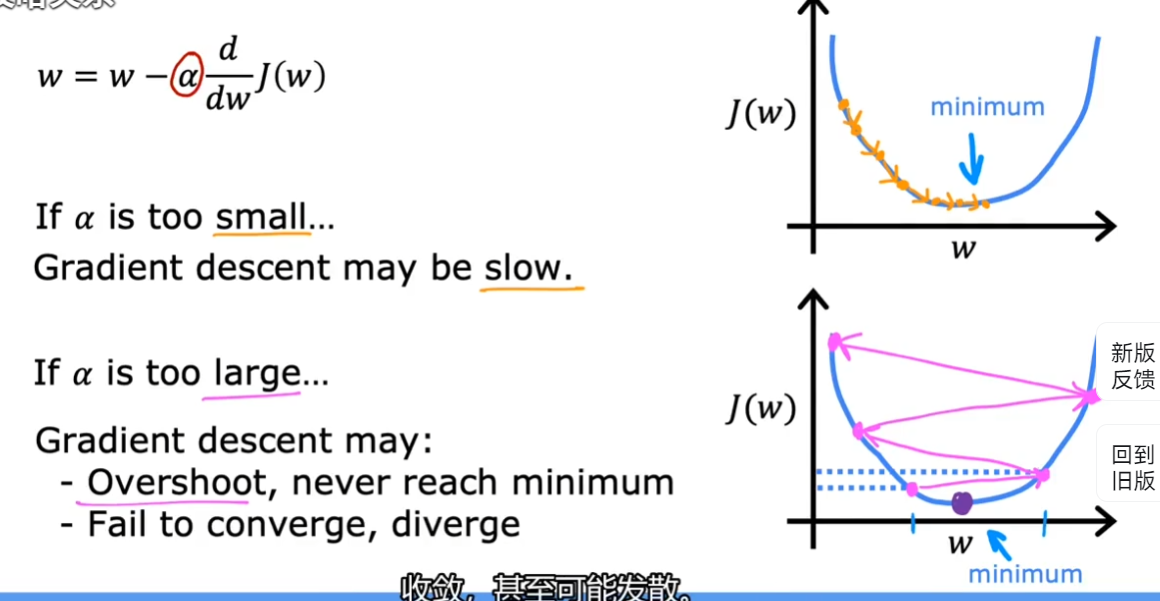
学习率太小：梯度下降太慢

学习率太大：可能无法收敛，反而发散

1.6.1.1. 如何选择好的学习率

debug 梯度下降的方法是：将学习率设定为非常小，然后看迭代后 J 是否收敛（向极小值/最小值逼近）

1.6.2. 批量梯度下降

Batch gradient descent

‘Batch’的意思是梯度下降的每一步都使用所有的训练集

1.6.3. 矢量化

多元线性回归

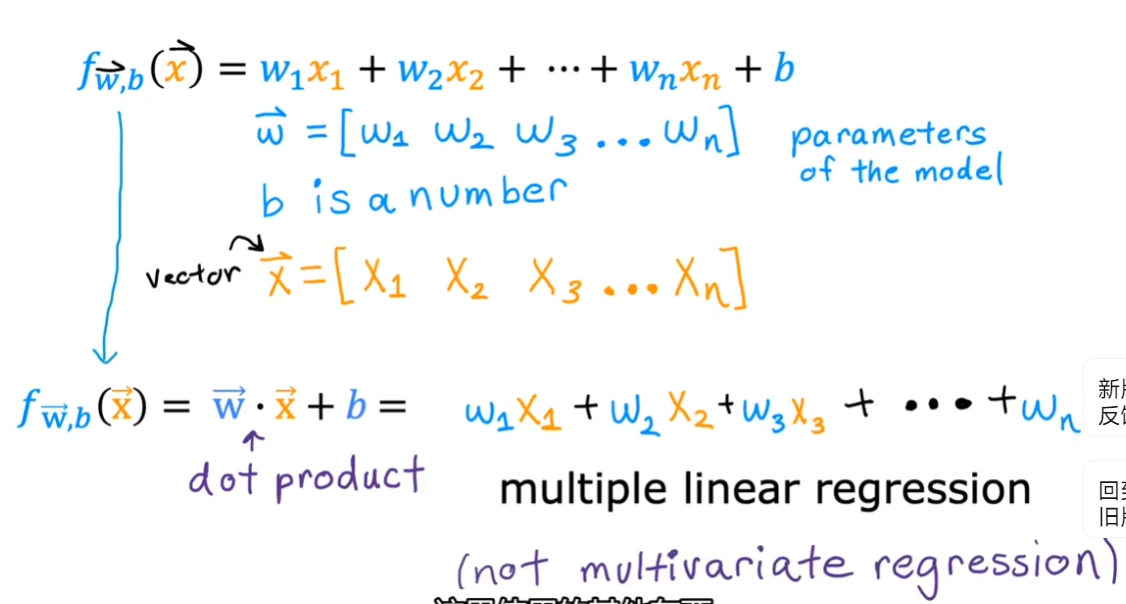
矢量化快速的原因主要是可以理由计算机的并行硬件进行并行计算，而 for 循环只能在循环中一个个循环的计算。

1.6.4. 多元回归的梯度下降

1.7. 正规方程法

normal equation
只针对线性回归，不需要迭代即可求解 w 和 b 的方法
不适用其他方法
当 features 很大（> 10000）时，处理很慢

1.8. 特征缩放

让梯度下降更快
让多维数据彼此之间的范围变得 comparable
归一化（mean normalization），让所有参数在[-1, 1]之间

$$
x_i = \frac{x_i - μ_i}{max - min}
$$

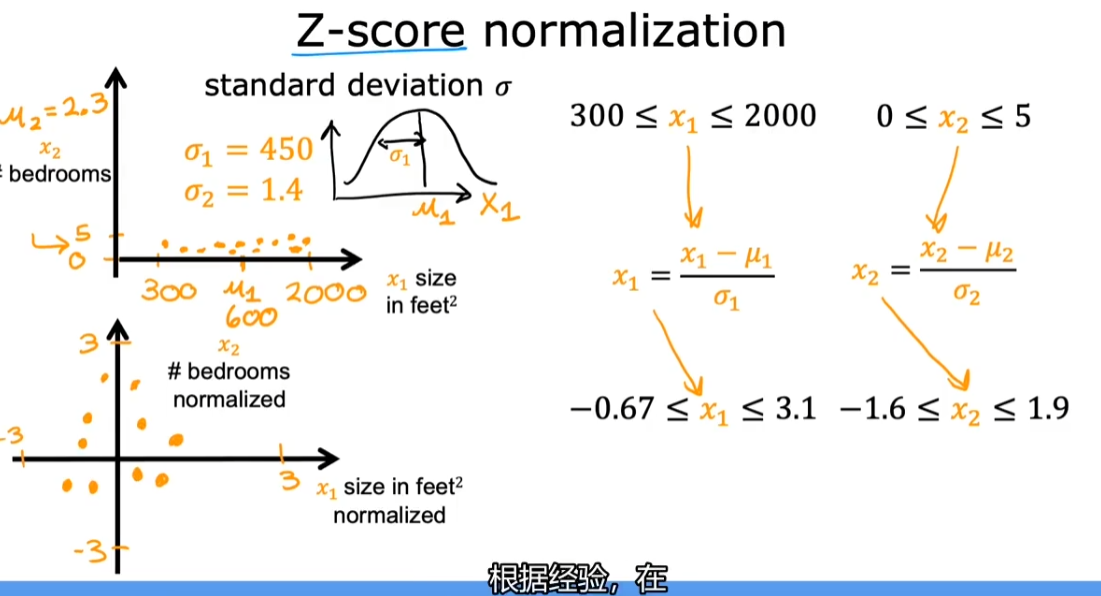
Z-scroe 归一化（normalization）
计算每个特征的标准差

$$
X_i = \frac{x_i - μ_i}{\sigma_i}
$$

一样可以达到让所有参数在[-1, 1]之间

1.9. 检查梯度下降 work well

通过学习曲线（绘制 J-iteration 函数图像）观察函数变平的时候
通过自动收敛测试。其实很类似微积分证明极限的思想。当 J 每次增减小于 δ（极小）时，认为已经收敛

1.10. 特征工程

Feature engineering
通过直觉来设计一个新特征，通常通过改变或结合已有特征来实现
选择正确且适当的特征是机器学习模型 work well 的重要前提

1.11. 多项式回归

Polynomial regression
即使用高次、开根等项进行回归拟合

May 03, 2022

Coursera: ML01-概论与线性回归